Simulating the Monty Hall problem

Of course it's been done before, but I wanted to do it anyway.

Recently my wife and I have been binge watching Brooklyn Nine-Nine and we just watched the episode where Santiago, Holt, and Kevin are all involved in an argument about the Monty Hall problem.

In short: You are on a game show and behind one of three doors is a car. You pick a door. Then the host, who knows which door the car is behind, opens one of the losing doors and asks you if you want to switch doors. Do you switch doors?

The argument is overall an argument of the probability. Are you more likely to win by keeping the door you originally selected or switching doors? Or does it not matter?

Instead of arguing over probabilities this can be easily simulated in code.

Here are a few helper functions to play the game:

# Designate a winning door
def make_winning_door():
    return np.random.randint(0,3)

# Have the 'host' open a losing, but not selected door
def eliminate_wrong_door(winning_door: int, selected_door: int):
    doors = [0,1,2]
    doors.remove(winning_door)
    try:
        doors.remove(selected_door)
    except: 
        pass #silently fail
    
    return random.choice(doors)

# Give the option to switch to the other closed door
def switch_doors_choice(remaining_doors: list, selected_door: int, switch=False):
    assert len(remaining_doors) == 2, "Too many doors given"
    assert selected_door in remaining_doors, "Selected door already opened"
    
    if switch:
        remaining_doors.remove(selected_door)
        return remaining_doors[0]
    else:
        return selected_door

Now I used these functions in a loop to play the game 20,000 times. Switching doors 10,000 and not switching 10,000.

wins = []

for i in range(10000):

    doors = [0,1,2]

    ## Create the prize door
    winning_door = make_winning_door()

    ## Select a door
    selected_door = np.random.randint(0,3)

    ## Open one of the loosing doors
    doors.remove(eliminate_wrong_door(winning_door, selected_door))

    ## Switch or dont switch doors
    final_selected_door = switch_doors_choice(doors, selected_door, switch=False)

    ## Find out if you won
    if final_selected_door == winning_door:
        wins.append(1)
    else:
        wins.append(0)
        
wins_switch = []

for i in range(10000):

    doors = [0,1,2]

    ## Create the prize door
    winning_door = make_winning_door()

    ## Select a door
    selected_door = np.random.randint(0,3)

    ## Open one of the loosing doors
    doors.remove(eliminate_wrong_door(winning_door, selected_door))

    ## Switch or dont switch doors
    final_selected_door = switch_doors_choice(doors, selected_door, switch=True)

    ## Find out if you won
    if final_selected_door == winning_door:
        wins_switch.append(1)
    else:
        wins_switch.append(0)

Running this simulation shows you have a 2/3 chance of winning by switching doors. Keeping your originally selected door only gives you a 1/3 change of winning.

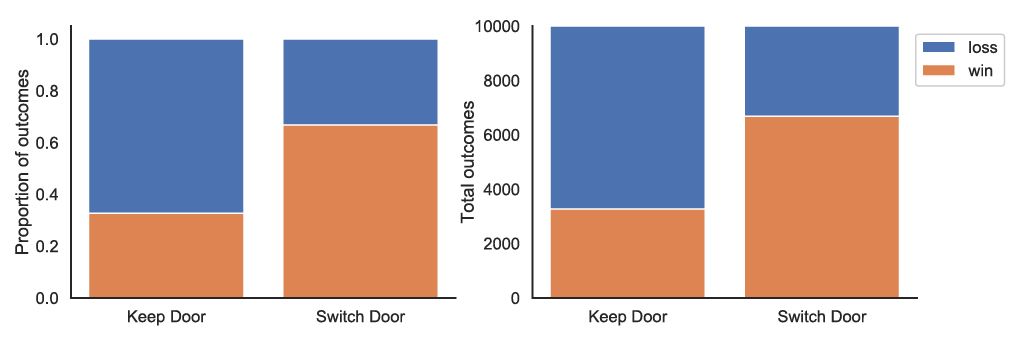
Amy Santiago was correct.